Air Properties

Whenever we deal with top level design or with some instrument detail engineering it is necessary to know air data properties. Air properties most relevant for air data applications are:

Air Density, $\rho$ , $kg/m^3$
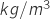
Vapor pressure, $psv$ , $Pa$
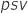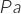
Dynamic Viscosity 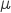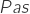$\mu$ , $Pas$ in SI; for ease of use 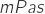$mPas$ are reported instead
Speed of sound $a$ , $m/s$

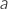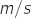
For standard air data measurements, for example, altitude, also air properties to be used are well defined. Often ISA atmosphere model is used; when a model is used it is possible to compare performances and general results among different designs.

Standard air properties are readily computable, and they are available on printed tables on many books; you can also find some online resources. The air properties are a function of pressure, temperature, and relative humidity; the widespread adopted ISA standard assumes that air is dry.

For example purposes we’re treating here the most general scenario; let’s pretend that we want to get a True Air Speed reading from a Pitot tube.

Our design goal is to have a really accurate air speed measurement; to do so we should measure also pressure and temperature to accurately calculate air density.

It’s possible to download commercial software. You find these free calculation routines from BasicAirData. You can install on your mobile device the free BasicAirData Android Air Properties app, available in this link.

An air state function can be written as $\rho=f(p,v,h)$ . That state function is invertible and correlates all the variables uniquely. The ideal state equation is not approximate in any way; it doesn’t introduce any uncertainty; whoever knows the value of involved variables knows the exact value of density. In a real world case, every measurement will have an unavoidable uncertainty, and even the state function have a correlated uncertainty.

There are different math models that can be used to calculate air density, we chose the CIPM 91 equation. That model is used, but not only, to manage buoyancy related problems during mass measurements. Air molecular weight is assumed to be constant, to increase accuracy it should be necessary to account for the air molecular weight variation with altitude. Air composition can be affected by local environmental conditions; also that aspect is neglected by the model, the air composition is assumed to be constant. CIPM can handle moist air, although is to be noted that measurements of the air humidity with airborne instrumentation are not trivial.

In many practical cases, as referenced here [1] (Paragraph 1.7), a direct application of Buckingham theorem leads to an important variable reduction. Assuming an incomprehensible flow, the aerodynamic behavior can be described by means of two nondimensional numbers Re and M. That notion comes handy when a laboratory calibration, for example for a multi-hole probe, is needed.

To calculate Reynolds number it is necessary to know the value of the dynamic viscosity, $Re=\frac{\displaystyle \rho TAS D_C}{\displaystyle \mu}$ . The Sutherland’s formula [1] (Paragraph 15.3) provides a well-proven method to calculate the viscosity, it seems appropriate for applications at ambient conditions.

Mach number $M$ is defined as the ratio between airspeed and speed of sound, $M=TAS/a$ .

The speed of sounds depends on many variables, however, there is an approximation based on the calorically perfect gas hypothesis [1](Formula 8.25)

$\gamma$ is the specific heat ratio, $R$ is the universal gas constant, $Mw_{air}$ is the molecular weight of air.

$a=\sqrt{\gamma R_{air}T}$

$R_{air}=R/Mw_{air}$

We have introduced the basic air properties, those properties will be enough to cover almost any example present into the site.

Apart from the calculation of properties by itself it is worthy to calculate also the correlated uncertainty. With the air density uncertainty value, it will be possible to numerically evaluate the TAS uncertainty. That calculation will be carried out in a specific numeric example.

References