
Air density ![]() is a typical case of measurement derived from air data. Let’s investigate the relationship between air temperature and air density, which, incidentally, is the base of the external air temperature measurement in moving vehicles.
is a typical case of measurement derived from air data. Let’s investigate the relationship between air temperature and air density, which, incidentally, is the base of the external air temperature measurement in moving vehicles.
Commonly the air density can be calculated with an equation of state or with an interpolated best-fit curve. In both cases, we have to deal with an equation of the form ![]() . Let’s make things a bit simpler and start with a simple relationship between density and temperature:
. Let’s make things a bit simpler and start with a simple relationship between density and temperature:
![]()
The temperature in the SI is measured in degrees Kelvin, but many equations of state may also be given with temperature expressed in ![]() .
.
Quoted from www.bipm.org: “The kelvin, unit of thermodynamic temperature, is the fraction 1/273.16 of the thermodynamic temperature of the triple point of water.”.
The thermodynamic temperature is correlated to the state of a thermodynamic system, and according to the third law of thermodynamics, it defines an absolute temperature scale.
For dry air, the ideal gas equation of state is: ![]() where:
where:
 is the air density in
is the air density in 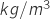
 is the absolute pressure in
is the absolute pressure in 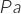
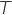 is the absolute temperature in
is the absolute temperature in 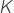
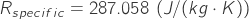 is the specific gas constant for air.
is the specific gas constant for air.
The main advantage of the equation of state is that it provides a closed form solution, which in turn can be incorporated in other computations. This is a very convenient property for analysis purposes. Let’s proceed with a density calculation. Refer to figure 1; our idealized test setup is a room with two thermometers and a fan. The first thermometer measures the temperature of the air in the room at a point far away from the fan effects, while the second one is subject to the direct airflow from the fan.
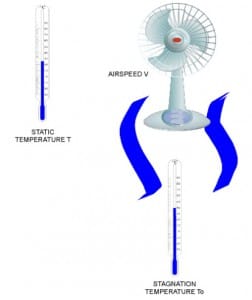
Figure 1 – Example layout
Before any calculation let’s introduce the stagnation temperature, which indicates the temperature at a stagnation point within a flow field. At the stagnation point, the local flow velocity is zero. We find a stagnation point on a Pitot tube tip or in a total air temperature probe.
In our example, the air from the fan which hits the thermometer is brought to rest on the surface of the sensing element. Consider an infinitesimal volume of the overall air stream traveling at a certain speed.
This small volume has a corresponding kinetic and gravitational potential energy. If we assume that this volume does not exchange any form of energy with the surroundings then this energy must be converted when one of its forms is eliminated. In the process where the air slows down, kinetic energy is converted into heat, which causes a temperature rise.
Assuming an adiabatic process we can describe the enthalpy at stagnation:
![]()
where:
- the enthalpy term
 is that of the nearest point along the streamline
is that of the nearest point along the streamline  is the speed of the air flow.
is the speed of the air flow.
For an ideal gas it holds that ![]() where:
where:
 is the specific volume
is the specific volume is the internal energy of the gas.
is the internal energy of the gas.
By manipulating the enthalpy expression and taking into account the constant pressure heat capacity definition ![]() for an ideal gas
for an ideal gas ![]() , we arrive at:
, we arrive at:
![]()
This equation defines how much the temperature rises because is adiabatically brought to rest.
Returning to our example let’s calculate the different values of stagnation temperature in correspondence of different airspeed values. You can find pre-calculated values in the table below.
| T [K] Static | V [m/s] | V [km/h] | M | T0 [K] Stagnation | Deviation [K] | Deviation [%] | Parameters | ||
|---|---|---|---|---|---|---|---|---|---|
|
288.15
|
0
|
0
|
0
|
288.15
|
0
|
0
|
Cp
|
1005
|
J/Kg/K
|
|
288.15
|
2
|
7.2
|
0.01
|
288.15
|
0
|
0
|
c
|
340.3
|
m/s
|
|
288.15
|
3
|
10.8
|
0.01
|
288.15
|
0
|
0
|
|||
|
288.15
|
4
|
14.4
|
0.01
|
288.16
|
-0.01
|
0
|
|||
|
288.15
|
5
|
18
|
0.01
|
288.16
|
-0.01
|
0
|
|||
|
288.15
|
6
|
21.6
|
0.02
|
288.17
|
-0.02
|
0.01
|
|||
|
288.15
|
7
|
25.2
|
0.02
|
288.17
|
-0.02
|
0.01
|
|||
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
By inspection of the table, the deviation between the two temperature measurements increases with the
The air density in the room should be calculated using the static temperature, in our case, e.g. ![]() the corresponding density is
the corresponding density is ![]() . The same calculation using the total temperature with a fan pushing the air at 55 m/s gives
. The same calculation using the total temperature with a fan pushing the air at 55 m/s gives ![]() , which is about a 0.5% of error on density.
, which is about a 0.5% of error on density.
Inspect the relationship between the static and total temperature for a total air temperature probe; the first formula in this link.
![]()
Where the “total” subscript indicates the adiabatic temperature and “s” subscript is for the static temperature. To reach this formula from our derived temperature equation, substitute in this formula the definition of the specific heat ratio ![]() , Mayer’s relation
, Mayer’s relation ![]() and the Mach number expression:
and the Mach number expression:
![]()
The total air temperature computed up to now here is somewhat ideal. All the kinetic energy is converted and contributes to a temperature rise, but it should be accounted with an appropriate recovery factor. The relationship of the recovery factor with airspeed and other environmental factors is not trivial, and for best accuracy, it should be experimentally found. Nonetheless, the tight relationship between airspeed and temperature can be exploited to have a true airspeed indication as per equation 9 in the previous link. Consequently, a total air temperature probe working together with a Pitot-static tube offers a useful redundant airspeed indication.
Even at low airspeeds, to achieve top performance, the temperature measurement rise due to airspeed is existent. However, the impact of this effect on temperature measurements can be neglected in many applications with moderate to no loss of accuracy. Unfortunately, this is not the only source of uncertainty in a total air temperature probe.
Further reading
- Full developed calculation example
0 Comments