Dew is water in the form of droplets, that forms on surfaces due to condensation. Ersa was the mythological Greek goddess of dew, and even if she cannot protect us from it anymore, her inheritance can impact on our basic air data measurements.
Dew point is the temperature at which dew forms. Knowledge of the dew point gives us a direct information on air humidity. This information can be useful by itself or when we need to check if dew will form during instrument operation. In particular, we needed to determine if dew can become a problem in a heated Pitot probe design.
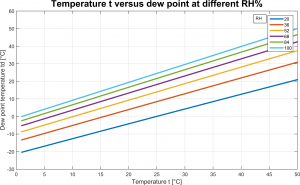
Moist air is a mix of dry air and water vapor. Speaking in terms of relative humidity (RH), the moist air dew point is reached when RH is equal to 100%. Relative humidity is defined as the ratio between the partial vapor pressure and the equilibrium vapor pressure. When the partial pressure reaches its maximum physical value it is equal to the equilibrium vapor pressure In this condition there is the maximum possible presence of water vapor in the air. Under these terms, it is evident that dew point is an equivalent expression to air humidity.
In order to determine this value we need to determine the saturation vapor pressure value first. Many methods[1] exist for vapor pressure calculation. We will use the one recommended in “Guide to Meteorological Instruments and Methods of Observation“ edited by the World Meteorological Organization 2012[2], formulas in ANNEX 4.B 1.4-29. Accuracy considerations deserve a dedicated treatment, somce this calculation method is not rated for extreme accuracy but has the advantage to be easy to implement.
Saturation vapor pressure in the pure phase with regard to water at the dry-bulb temperature is:
(1) 
with t in [°C] and 
in [hPa].
The saturation vapor pressure of moist air with regard to water at the dry-bulb temperature is:
![\[e^i_w= f(p) \cdot e_w(t)\]](http://www.basicairdata.eu/wp-content/ql-cache/quicklatex.com-85ce33b75a42b4783ac5b0ca21ef51bc_l3.png "Rendered by QuickLaTeX.com")
with 
From the reference[2] we get also the expression for relative humidity 
. We denote the dew point temperature as 
.
We can rewrite the humidity expression:
(2) 
This formula can be used for pressures around 100000 Pa, so at low MSL altitude. This approximation holds for the common RC aircraft operations. You can find a Matlab/Scilab script to calculate the vapor pressure here: [download id=”1148″].
Equation 2 is pretty interesting to us because it states that saturation vapor pressure of moist air at the dew point is always lower than saturation vapor pressure; inspect 1 and note that saturation vapor pressure increases for increasing 
. As limit case we have 
, for which the two saturation pressures are the same.
Figure 1 – Temperature Vs Dew point in function of RH
Figure 1 reports the relationship between dew point, temperature and relative humidity of moist air.
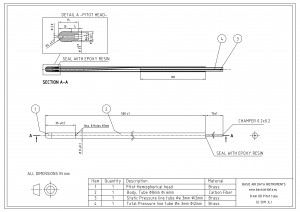
With that concise fact we can inspect our designs for areas of potential dew formation. Let’s consider a heated Pitot probe, such as the one in Figure 2, which has a metallic heated external pipe.
The external pipe is exposed to ambient temperature and ambient air can enter the probe from the total pressure and from the static holes.
Extremal scenarios are considered, with higher and lower external temperature. When external temperature is high, there is a risk of dew when the probe internal parts are at a temperature that is lower than the ambient air dew point. During normal operations the probe is not cooled in any way and the air flow through the pressure ports is really limited, so it’s not likely that dew will form.
On the other hand at low ambient temperatures, if the external pipe is heated, the internal air will be in contact with a surface with a temperature superior to its proper temperature; that excludes the possibility for dew formation. Are we safe from dew? Not at all.
Apart stationary conditions they can be transients: consider the case where the probe freezes, ice gathers on the probe, and then we suddenly move the probe to a warmer air region, while working with an unheated probe or with an inefficient heater. The external pipe will have a really low temperature and will cause the condensation of freshly introduced warm air. The same phenomenon can happen without the need to arrive to freeze point, but only passing from cold to warm conditions.
Figure 2 – Example Pitot Layout
In many cases if a drop of dew is found inside the Pitot-static probe the measurements will be disturbed. It would be really unlucky if water was formed within the pneumatic lines and reached the pressure sensor.
That can be avoided, not 100% cases, by using condensation traps. In RC applications it is advisable to simply place the sensor case at a height greater to that of the Pitot-static probe.